Các bài khác
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 1 Giá trị lượng giác của góc lượng giác
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 2 Công thức lượng giác
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 3 Hàm số lượng giác
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 4 Phương trình lượng giác cơ bản
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài tập cuối chương 1
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 5 Dãy số
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 6 Cấp số cộng
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 7 Cấp số nhân
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài tập cuối chương 2
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 8 Mẫu số liệu ghép nhóm
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 9 Các số đặc trưng đo xu thế trung tâm
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài tập cuối chương 3
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 10 Đường thẳng và mặt phẳng trong không gian
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 11 Hai đường thẳng song song
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 12 Đường thẳng và mặt phẳng song song
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 13 Hai mặt phẳng song song
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 14 Phép chiếu song song
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài tập cuối chương 4
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 15 Giới hạn của dãy số
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 16 Giới hạn của hàm số
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 17 Hàm số liên tục
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài tập cuối chương 5
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài HĐ thực hành trải nghiệm 1 Một vài áp dụng của Toán học trong tài chính
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài HĐ thực hành trải nghiệm 2 Lực căng mặt ngoài của nước
- Toán 11 kết nối tri thức: Tải slide trình chiếu bài 18 Luỹ thừa với số mũ thực
Toán 11 kết nối tri thức: Tải slide trình chiếu bài 11 Hai đường thẳng song song
Mẫu giáo án powerpoint, giáo án điện tử, slide trình chiếu toán 11 kết nối tri thức. Chi tiết bài 11 Hai đường thẳng song song. Bài giảng này được thiết kế hấp dẫn, cuốn hút. Các nội dung chính được trình bày cô đọng, dễ nhớ. Giáo án dùng để chiếu lên tivi, máy chiếu dạy cho học sinh. Tải về đơn giản, dễ dàng
Nội dung giáo án










......
=> Phía trên chỉ là một phần. Giáo án khi tải về có đủ nội dung bài học
Nội dung chính trình bài trong Slides
CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC HÔM NAY!
KHỞI ĐỘNG
Để giải quyết vấn đề tắc đường ở các thành phố lớn, có rất nhiều giải pháp được đưa ra. Trong đó giải pháp xây dựng các hệ thống cầu vượt, đường hoặc đường sắt trên cao đã và đang được đưa vào thực tế ở Việt Nam. Toán học mô tả vị trí tương quan giữa các tuyến đường trên như thế nào?
CHƯƠNG IV. QUAN HỆ SONG SONG TRONG KHÔNG GIAN
BÀI 11. HAI ĐƯỜNG THẲNG SONG SON
NỘI DUNG BÀI HỌC
Vị trí tương đối của hai đường thẳng
Tính chất của hai đường thẳng song song
Nhắc lại kiến thức, làm bài tập
- VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG
HĐ 1:
Quan sát bốn tuyến đường trong Hình 4.13 và trả lời câu hỏi sau:
- a) Hai tuyến đường nào giao nhau?
- b) Hai tuyến đường nào không giao nhau?
- c) Hai tuyến đường nào song song?
Trả lời:
Quan sát Hình 4.13 ta thấy:
- a) Hai tuyến đường mũi tên màu đỏ và mũi tên màu vàng giao nhau.
- b) Hai tuyến đường mũi tên màu xanh dương và màu xanh lá cây không giao nhau.
- c) Hai tuyến đường mũi tên màu xanh dương và mũi tên màu đỏ song song.
KẾT LUẬN
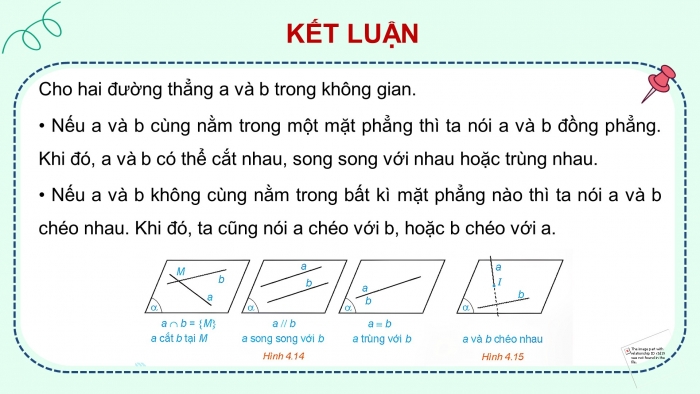
Cho hai đường thẳng a và b trong không gian.
- Nếu a và b cùng nằm trong một mặt phẳng thì ta nói a và b đồng phẳng. Khi đó, a và b có thể cắt nhau, song song với nhau hoặc trùng nhau.
- Nếu a và b không cùng nằm trong bất kì mặt phẳng nào thì ta nói a và b chéo nhau. Khi đó, ta cũng nói a chéo với b, hoặc b chéo với a.
Câu hỏi
Hãy tìm một số hình ảnh về hai đường thẳng song song, hai đường thẳng chéo nhau trong thực tiễn.
Ví dụ:
- Hình ảnh hai đường thẳng song song:
Hai cạnh đối diện của chiếc bàn
Vạch kẻ đường
- Hình ảnh hai đường thẳng chéo nhau:
Cạnh bàn và đường nối chân bàn
Nhận xét
- Hai đường thẳng song song là hai đường thẳng đồng phẳng và không có điểm chung.
- Có đúng một mặt phẳng chứa hai đường thẳng song song.
Ví dụ 1:
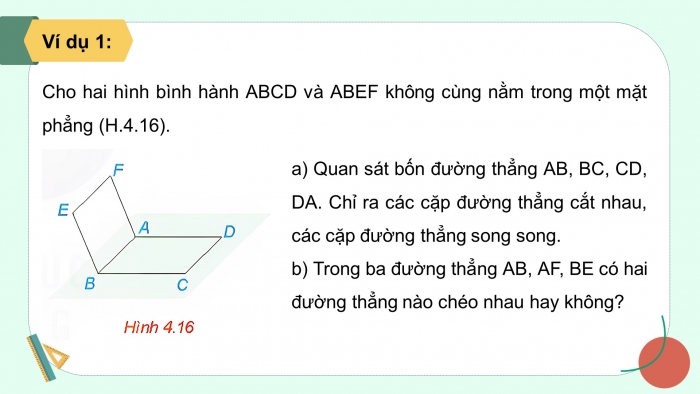
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng (H.4.16).
- a) Quan sát bốn đường thẳng AB, BC, CD, DA. Chỉ ra các cặp đường thẳng cắt nhau, các cặp đường thẳng song song.
- b) Trong ba đường thẳng AB, AF, BE có hai đường thẳng nào chéo nhau hay không?
Giải
- a) Các cặp đường thẳng cắt nhau là AB và BC, AB và DA, BC và CD, CD và DA.
Các cặp đường thẳng song song là AB và CD, DA và BC.
- b) Các đường thẳng AB, AF, BE cùng nằm trong mặt phẳng (ABEF) nên trong ba đường thẳng đó không có hai đường thẳng nào chéo nhau.
Luyện tập 1
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (H.4.17)
- a) Trong các đường thẳng AB, AC, CD, hai đường thẳng nào song song, hai đường thẳng nào cắt nhau?
- b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh SA, SB. Trong các đường thẳng SA, MN, AB có hai đường thẳng nào chéo nhau hay không?
Giải
- a) Hai đường thẳng AB và AC cắt nhau tại giao điểm A.
Hai đường thẳng AB và CD song song với nhau (do ABCD là hình bình hành).
Hai đường thẳng AC và CD cắt nhau tại giao điểm C.
- b) Vì hai điểm M, N lần lượt là hai điểm thuộc hai cạnh SA, SB nên hai điểm M, N thuộc mặt phẳng (SAB) hay các điểm S, A, B, M, N cùng thuộc một mặt phẳng nên các đường thẳng SA, MN, AB đồng phẳng, do đó khi lấy bất kì 2 trong 3 đường thẳng trên thì chúng có thể cắt nhau hoặc song song hoặc trùng nhau.
Vậy trong các đường thẳng SA, MN, AB, không có hai đường thẳng nào chéo nhau.
Ví dụ 2:
Cho hình tứ diện ABCD (H.4.18). Hai đường thẳng AB và CD có chéo nhau hay không? Chỉ ra các cặp đường thẳng chéo nhau có trong hình tứ diện đó.
Giải
Nếu hai đường thẳng AB và CD không chéo nhau thì chúng cùng thuộc một mặt phẳng.
Khi đó bốn điểm A, B, C, D đồng phẳng, trái với giả thiết ABCD là hình tứ diện.
Do đó, hai đường thẳng AB và CD chéo nhau.
Lập luận tương tự, ta thấy trong tứ diện ABCD còn có các cặp đường thẳng chéo nhau là AC và BD, AD và BC.
Luyện tập 2
Trong hình chóp tứ giác S.ACBD (H.4.19), chỉ ra những đường thẳng:
- a) Chéo với đường thẳng SA;
- b) Chéo với đường thẳng BC
Giải:
- a) Các đường thẳng chéo với đường thẳng SA là BC và CD.
Giải thích: Nếu hai đường thẳng SA và BC không chéo nhau thì chúng cùng thuộc một mặt phẳng. Khi đó bốn điểm S, A, B, C đồng phẳng, trái với giả thiết S.ABCD là hình chóp. Do đó, hao đường thẳng SA và BC chéo nhau. Tương tự, giải thích được hai đường thẳng SA và CD chéo nhau.
- b) Các đường thẳng chéo với đường thẳng BC là SA và SD. Giải thích tương tự câu a.
Vận dụng 1
Thông tin tải tải liệu
Nhận xét
Đánh giá trung bình
Chi tiết
Kho tài liệu Toán 11 kết nối tri thức
Giáo án lớp 11 kết nối tri thức chương trình mới bản chuẩn
1. Giáo án ban tự nhiên
- Giáo án toán 11 kết nối tri thức chuẩn nhất
- Giáo án vật lí 11 kết nối tri thức chuẩn nhất
- Giáo án sinh học 11 kết nối tri thức chuẩn nhất
- Giáo án hoá học 11 kết nối tri thức chuẩn nhất
- Giáo án tiếng anh 11 kết nối tri thức chuẩn nhất
2. Giáo án ban xã hội
- Giáo án ngữ văn 11 kết nối tri thức chuẩn nhất
- Giáo án lịch sử 11 kết nối tri thức chuẩn nhất
- Giáo án Địa lí 11 kết nối tri thức chuẩn nhất
- Giáo án kinh tế pháp luật 11 kết nối tri thức chuẩn nhất
3. Giáo án các môn khác
- Giáo án quốc phòng 11 kết nối tri thức chuẩn nhất
- Giáo án mĩ thuật 11 kết nối tri thức chuẩn nhất
- Giáo án thể dục 11 kết nối tri thức chuẩn nhất
- Giáo án tin học 11 kết nối tri thức chuẩn nhất
- Giáo án Âm nhạc 11 kết nối tri thức chuẩn nhất
- Giáo án công nghệ 11 kết nối tri thức chuẩn nhất
- Giáo án Hoạt động trải nghiệm 11 kết nối tri thức chuẩn nhất
